Три місяці тому («День» за 28 серпня ц. р.) один із авторів цієї статті оприлюднив відкритий лист до кандидатів на посаду президента України та голови ЦВК С. Ківалова. Йшлося про співробітництво в проведенні математичної експертизи загальнодержавних протоколів, які віддзеркалюють підсумки голосування. Така експертиза дозволяє діагностувати відсутність (наявність) ознак застосування адміністративного ресурсу, маніпуляцій списками виборців, бюлетенями чи виборчими протоколами. Відтак експертні оцінки дозволяють інформувати виборців про те, з якою мірою довіри вони можуть сприймати офіційну інформацію про підсумки голосування. За таких умов жоден кандидат на посаду президента України, який програв у чесній боротьбі, не матиме підстав для політичних спекуляцій. Водночас переможець може не зважати на звинувачення опонентів — але тоді і лише тоді, коли математичний показник аномальності (об’єктивний за своєю сутністю) не відхилятиметься від нуля.
ЦИФРОВИЙ АНАЛІЗ
Якщо ви, шановний читачу, взяли до рук книгу, яка має 1000 сторінок, то обов’язково матимете в ній 50% сторінок парних (2, 4, 6…. 1000) і 50% непарних (1, 3, 5… 999). Якщо ж у друкарні щось наплутали, то може виявитися не 50% +50% , а, скажімо, 60% + 40%. Щоб упевнитися у відсутності браку, не обов’язково додивлятися до чисел, якими позначені сторінки (наприклад, 743, 744, 745 і т. д.). Достатньо глянути на останню цифру кожного числа (3, 4, 5 і т.д.), за якою ми розпізнаємо парність і непарність. Цей школярський приклад ілюструє сутність цифрового аналізу. Новітнім надбанням теорії ймовірностей і математичної статистики є т. зв. принцип Бенфорда. Він стосується частотного розподілу цифр у природному (naturalness) числовому масиві, який віддзеркалює сутність чи явище, що склалися органічно («стихійно»). Формула Бенфорда 1) є математичною характеристикою різноманітних ситуацій, які вивчають соціологи, ботаніки, географи, астрономи, фізики, лінгвісти тощо. Читачам, які зацікавилися цією проблемою, можемо рекомендувати (і подарувати) написану нами монографію. 2) Останні 5 років в науковій літературі зростає кількість публікацій про те, що відхилення від бенфордівського стандарту свідчить про фальшування податкових декларацій та банківських документів. Наші дослідження показали інформативність такого підходу до матеріалів, що їх оприлюднила ЦВК після парламентських і президентських виборів 1998—2002 років. 3) Сьогодні будемо говорити про експертизу підсумків 2-го туру голосування, оголошених ЦВК 24 листопада ц.р. Йдеться про 225 виборчих округів і Закордонний виборчий округ.
ЕЛЕКТОРАЛЬНИЙ ЗЛАМ
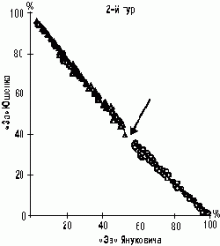
Маючи 226 чисел по кожному з двох кандидатів, насамперед мусимо перевірити, чи цей масив є внутрішньо єдиним (гомогенним). На графіку бачимо, що йдеться про два електоральних фрагменти (на першому кожний виборчий округ позначений трикутником, на другому — кружечком). Суцільні лінії (лінії регресії) віддзеркалюють усереднені статистичні тенденції. Бачимо, по-перше, «дірку» (позначену стрілкою), яка є особливо виразною на тлі того, як густо ліпляться один до одного трикутники й кружечки. Бачимо, по-друге, різний нахил (крутизну) двох ліній регресії. Не важко здогадатися, що перший фрагмент (120 округів, позначимо його буквою А) поєднує Захід, Центр і Північ держави, а другий фрагмент (106 округів, Б) — Південь і Схід. Самотній трикутник на їх межі — округ №26; решта його «побратимів» по Дніпропетровщині однозначно приєдналися до фрагменту Б.
Якщо говорити про математику, маємо свідчення того, що йдеться не про один, а про два числові масиви, і мусимо їх аналізувати нарізно. Для соціолога це відлуння трагедії, зумовленої історичними відмінностями соціальної психології (ментальності), і сьогоднішніми «досягненнями» тих політтехнологів, які саме на електоральному зламі заробили свої гроші.
ФАЛЬШ
У науці (і в матстатистиці зокрема) діє «принцип недоведеності». Коли політики кажуть про те, що підсумки виборів є сфальшовані, мусять мати докази. Вочевидь, мають їх, якщо йдеться про окремі виборчі дільниці чи навіть округи. Але ми торкнемося лише того, що ґрунтується на власному математичному дослідженні підсумкового загальнодержавного протоколу. В ланцюжку «принцип Бенфорда — формула Бенфорда — цифровий аналіз» останньою ланкою є т. зв. критерій Пірсона (хі-квадрат). Спираючись на нього, можемо визначити головне: чи відхилення числових масивів від математичного стандарту є такими, що лежать у межах статистичної похибки? Чи йдеться про грубі аномалії (дефекти), зумовлені фальшуванням? З глибоким сумом сповіщаємо, що у протоколах обох кандидатів і по обом електоральним фрагментам критерій Пірсона зашкалює. Для кожного з чотирьох підрахунків ймовірність того, що має місце саме фальсифікація, а не випадкові (несистематичні) помилки, перевищує 9999 із 10000 (див. табл.).
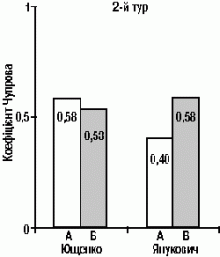
Особливістю критерію Пірсона є його залежність від розмірів числового масиву, для якого ведуться підрахунки. Виходячи з того, що фрагменти А і Б охоплюють неоднакову кількість виборчих округів (120 проти 106), мусимо вирівняти (математики кажуть — нормувати) показники аномальності. Для цього слугує т. зв. коефіцієнт Чупрова. Для нас він цікавий ще й тим, що може коливатися у вузькому діапазоні від 0 (математичний ідеал) до 1 (абсолютна фальш). Другий рисунок свідчить, що підсумки 2-го туру, оголошені ЦВК, є — кажучи м’яко — далекими від ідеалу.
Найцікавішою для всіх є відповідь на такі запитання: кому приписували, а кому недописували голоси? де брали, а де «отоварювали» відкріпні талони? на чию користь працювали «каруселі» й вкидалися «ліві» бюлетені? Мусимо розчарувати шановних читачів. Цифровий аналіз засвідчує наявність (відсутність) аномалій, але не дозволяє показати пальцем на їх замовника. Кожний дослідницький метод має свої обмеження, і з цим треба миритися. Втім, читачі можуть поміркувати над тим, що коефіцієнт Чупрова, розрахований по виборчих протоколах В. Ющенка, практично однаковий в електоральних полях А і Б. Натомість аномальність протоколів В. Януковича в зоні його перемоги більша, ніж на решті України.
Кандидат Критерій Пірсона Примітка
В. Ющенко А 80,0 аномалія
Б 59,7 аномалія
В. Янукович А 38,3 аномалія
Б 71,0 аномалія
1) Формула Бенфорда визначає кількість чисел, першою цифрою яких є 1,2,3…9. Якщо d — цифри від 1 до 9 включно, а Pd — частота кожної з них, то маємо: Pd = Log10(1+1/d). Відтак кількість чисел, які починаються на 1, дорівнює 0,301 (30,1%), на 2 — 0,176 (17,6%), і так далі. Чільних цифр 9 маємо лише 0,046 (4,6%).
Розглянемо конкретний приклад. Таблиця про крос-курси світових валют вміщує 160 чисел. Взаємна залежність між економіками 33 країн, репрезентованих у таблиці, упорядкованість їхніх імпортно-експортних потоків тощо дозволяють припустити, що йдеться не про окремі незалежні числа, а про їх природний масив. Відтак помноживши 160 на 0,301 і 0,046, знайдемо теоретичну кількість чисел, які мають першою цифрою відповідно 1 і 9. Ось розрахунок:
має бути цифр 1 — 50,
є фактично — 50
має бути цифр 9 — 7,
є фактично — 10
Відхилення фактичної кількості цифр 9 від розрахункової (10 проти 7) не перевищує статистичної похибки.
2) «Принцип Бенфорда. Цифровий аналіз», Київ, 2001, 64 с.
3) «Математична експертиза аномалій у виборчих протоколах» (Київ, 1999); «Виборчі технології у дзеркалі математики» (Київ, 2000); «Вибори- 2002. Нариси з політичної арифметики» (Київ, 2002)